When a Bose-Einstein condensate (BEC) is trapped in a double-well potential, it can perform quantum coherent oscillations between the wells, so-called Josephson oscillations. It is a fundamental problem of quantum statistical mechanics if and how such a non-equilibrium system can eventually come to rest and reach thermodynamic equilibrium. Since the quantum system is ideally isolated from its environment and, thus, evolves in time in a unitary way (i.e., the initially pure quantum state of the entire systems must remain a pure state for all times).
We show that the thermalization happens in that single bosonic atoms, so-called quasiparticles, get excited out of the condensate. This cloud of quasiparticles thermalizes by exchanging energy and particles with the BEC, thereby maximizing the entanglement entropy (the entropy associated with the entanglement of the quasiparticle states with the condensate state). That is, the BEC acts as a grand canonical reservoir for the quasiparticle subsystem. The dynamics of this thermalization process exhibits three distinct time scales: (I) an initial period of undamped Josephson oscillations, (II) a period of fast quasiparticle creation out of the BEC due to a dynamically generated, parametric resonance, and (III) a regime of slow thermalization of the quasiparticle gas.
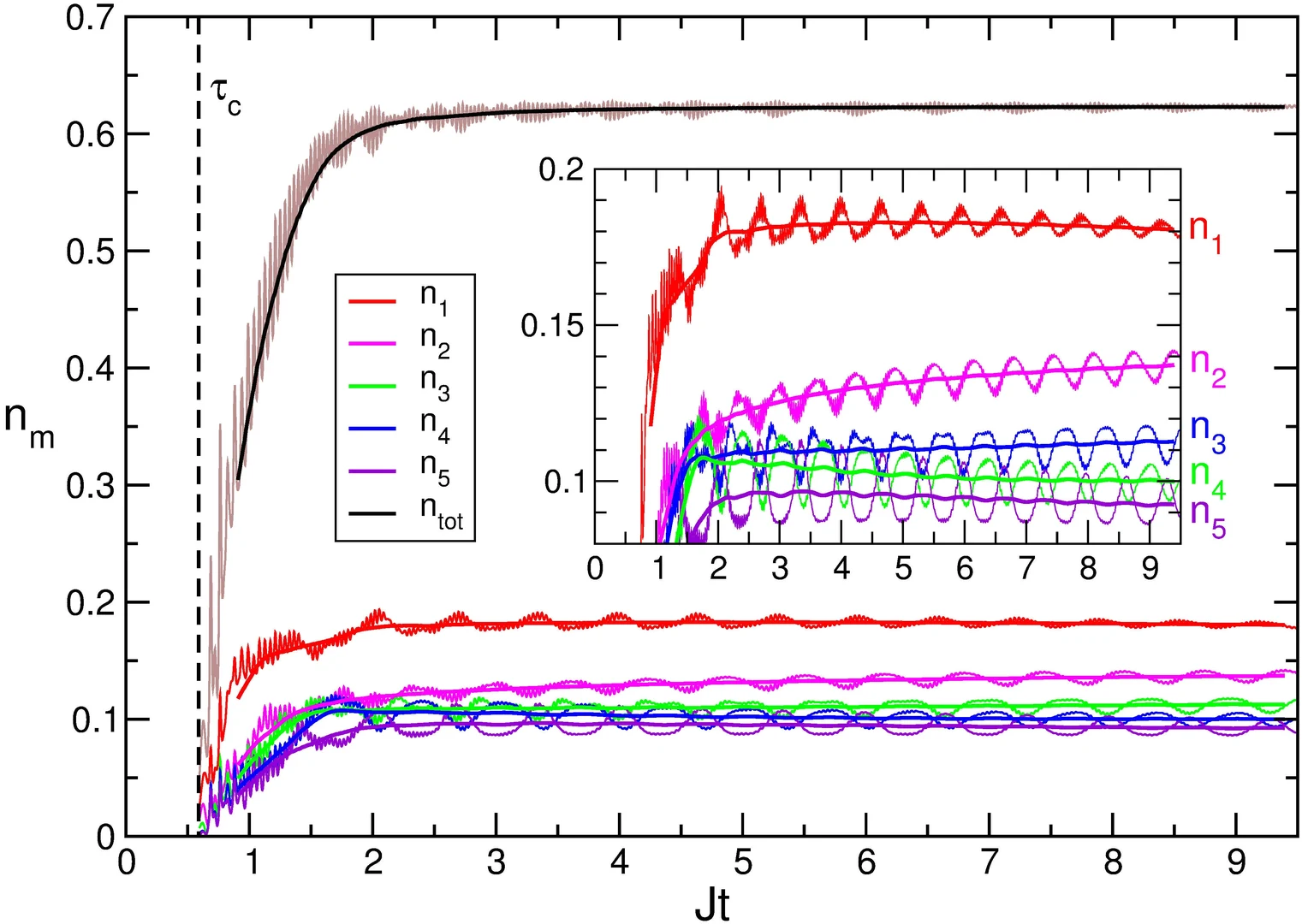
The picture shows the time-dependent population of the first five quasiparticle states as well as the total population. This dynamics bears similarities to the creation of elementary particles, as it is thought to have happened during the inflation and reheating periods of the early universe.